Kleines Astronomie-Glossar

Vorbemerkungen | Glossar | Links

Auf dieser Seite sammle ich einige nützliche Definitionen astronomischer Begriffe in einem kleinen Glossar und gebe einige entsprechende Links an. Bei Teleskopen beschränke ich mich im wesentlichen auf Dobson-Teleskope.

Übersicht der Begriffe

Äquatorial-Plattform (EQ-Plattform, Nachführ-Plattform, Tracking Platform), Äquatoriales Koordinatensystem, Azimutale (Alt-Azimutale) Montierung, Auge-Okularabstand (Eye Relief), Austrittspupille,
Auflösung,
Beugungsscheibchen (Airy Disk),
Deep Sky, Deep-Sky-Objekte, Deklination, Dobson-Teleskop,
Eintrittspupille, Ekliptik,
Himmelsäquator, Himmelspole,
Lichtsammelleistung,
Montierung,
Newton-Teleskop/-Reflektor,
Öffnung (Apertur), Öffnungsverhältnis,
Parallaktische (Äquatoriale) Montierung,
Rektaszension,
Seeing, Sehwinkel (Gesichtsfeld),
Vergrößerung, Maximal (sinnvoll) nutzbare Vergrößerung/Förderliche Vergrößerung, Maximalvergrößerung, Minimal (sinnvoll) nutzbare Vergrößerung

Kursiv: In Vorbereitung

Hinweis: Siehe auch Seite Rechenformeln für Teleskope für weitere Informationen, Formeln und Beispiele.

Vorbemerkungen

Das folgende Glossar erhebt überhaupt keinen Anspruch auf Vollständigkeit, denn es gibt im Internet genügend gute Informationsquellen. Die Glossardefinitionen, die ich hier aufführe, beziehen sich insbesondere auf die Teleskope, die ich auf dieser Website beschreibe, und sind nützlich für das Verständnis ihrer Eigenschaften.

In diesem Glossar lehne ich mich vor allem an Wikipedia-Definitionen an, die aber oft wenig verständlich sind. Ich habe deshalb versucht, die Texte umzuformulieren und verweise in den Referenzen auf entsprechende Artikel in Wikipedia und anderswo.

Glossar

Äquatorial-Plattform (EQ-Plattform, Nachführ-Plattform, Tracking Platform)

Dobsons sind alt-azimutale Teleskope und deshalb bei höheren Vergrößerungen von Hand nicht einfach nachzuführen. Äquatorial-Plattformen, 1977 von Adrien Poncet vorgeschlagen und seitdem von vielen anderen weiterentwickelt, lösen dieses Problem. Eine Äquatorial-Plattform dient als parallaktisch montierter flacher Unterbau, auf den der Dobson-Teleskop mitsamt seiner Rockerbox gestellt wird. Die Plattform ersetzt somit das Bodenbrett des Dobsons. Die intuitive Bedienung des Dobsons bleibt auch auf einer Plattform unverändert erhalten.

Äquatorial-Plattformen führen das Teleskop in der Regel etwa eine Stunde lang automatisch nach, dann müssen sie wieder zurückgestellt werden. Als Antrieb dient ein einfacher Elektromotor, der meist mit einer 9V-Blockbatterie betrieben wird.
(Nach: Reiner Vogel, angepasst)

Links:

Äquatorial-Plattform (Reiner Vogel): www.reinervogel.net/index.html?/Plattform/Plattform.html
EQ-Plattform (Dieter Martini): www.dietermartini.de/eqp.html

Äquatoriale Montierung

Siehe Parallaktische (Äquatoriale) Montierung

Äquatoriales Koordinatensystem

Als äquatoriales Koordinatensystem bezeichnet man zwei in der sphärischen Astronomie verwendete geozentrische Koordinatensysteme auf der Himmelskugel:

das rotierende (verwendet in Sternkarten) und
das ortsfeste äquatoriale Koordinatensystem (abhängig vom Benutzerstandort).

Die Bezugsebene ist in beiden Fällen die Ebene des Himmelsäquators.

Bezugspunkt auf dem Himmelsäquator ist beim rotierenden System der Frühlingspunkt (Tag-und-Nachtgleiche im Frühling), beim ortsfesten System der Schnittpunkt zwischen Himmelsäquator und Meridian des Beobachtungsorts.

Die Koordinaten im rotierenden System werden Deklination und Rektaszension genannt.
(Aus: Wikipedia, www.hobby-astronomie.com, verändert)

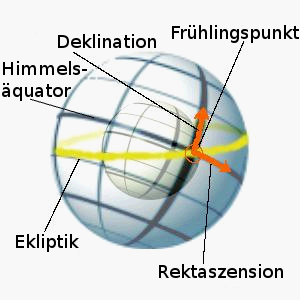
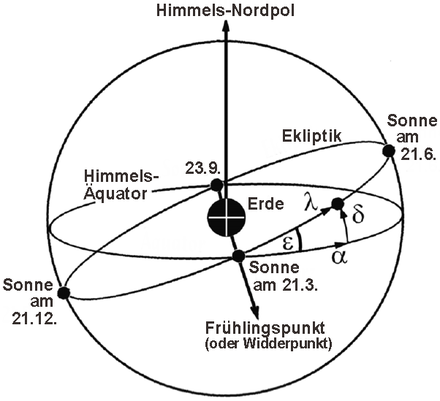
Bild: Äquatoriales Koordinatensystem (Quellen: Wikipedia, ursprünglicher hochladender Benutzer: Sverdrup (veränderte das Original von Ulrich.fuchs); Wikipedia, ursprünglicher hochladender Benutzer: Geof; beide unter CC-Lizenz)

Siehe auch Astronomische Koordinatensysteme (Wikipedia)

Auflösung

Auflösung wird definiert als die Möglichkeit, zwei eng beieinanderstehende Objekte (z.B. Doppelsterne) noch getrennt abzubilden. Hierfür gibt es zwei Kriterien:

Rayleigh-Kriterium: Beugungsscheiben berühren sich nicht
Dawes-Kriterium: Beugungsscheiben erzeugen 8-Bild

In der Paxis werden für beide Kriterien Faustformeln verwendet. Deshalb lasse ich die komplexe Mathematik hier einfach weg. Die beiden Faustformeln sind:

Rayleigh-Kriterium: Auflösung des Teleskops (") α = 138 / Öffnung (Objektiv-/Spiegeldurchmesser in mm)
Dawes-Kriterium: Auflösung des Teleskops (") α = 116 / Öffnung (Objektiv-/Spiegeldurchmesser in mm)

Die Auflösung hängt also allein von der Teleskop-Öffnung ab. Offensichtlich gilt das Dawes-Kriterium als "praxisgerechter" (siehe dazu den Artikel von Stefan Gotthold), und auch die Hersteller geben diesen Wert an (vermutlich auch, weil er günstiger aussieht).

Beispiel-Tabelle mit nach "Faustformel" berechneten Werten und Herstellerangaben

Teleskop	Brennweite*	Öffnung	Rayleigh	Dawes	Herstellerwert
Refraktor	400...700	60	2,3"	1,93"
S-W Heritage 76	300	76	1,82"	1,53"	1,51"
Refraktor	500...900	80	1,725"	1,45"
Meade ETX 90EC	1250	90	1,53"	1,29"	1,3"
S-W Heritage 100P	400	100	1,38"	1,16"	1,15"
S-W Skymax-102	1300	102	1,35"	1,14"	1,15"
S-W Skymax-127	1500	127	1,08"	0,91"	0,91"
S-W Explorer 150PDS	750	150	0,92"	0,77"	0,77"
GSO GSD 680	1200	200	0,69"	0,58"	0,58"
Meade Lightbridge 10"	1270	254	0,54"	0,46"	0,45"

*) Ohne Bedeutung hier

Hinweis: Üblicherweise ist die Auflösung bei der visuellen Beobachtung durch die Luftunruhe in der Atmosphäre auf ca. 1" begrenzt und nur in seltenen Ausnahmefällen besser. Das bedeutet, dass Fernrohre, die eine Öffnung von über 120 mm* haben, keinen echten Gewinn hinsichtlich der Auflösung bringen. (Astroshop, Oden)

*) 120 mm scheint sich auf die Dawes-Auflösung zu beziehen.

Auflösung am Mond

Die obigen Auflösungsformeln gelten für feine Strukturen wie z.B. Doppelsterne. Für den Mond gibt Lambert Spix im Buch Moonhopper folgende empirisch ermittelte Formeln an, die wesentlich höheren Auflösungen entsprechen, also das Erfassen wesentlich kleinerer Strukturen ermöglichen:

Dunkle Punkte vor hellem Hintergrund (Krater): Auflösung des Teleskops (") α = 39 / Öffnung (Objektiv-/Spiegeldurchmesser in mm)
Schwarze Linien vor hellem Hintergrund (Rillen): Auflösung des Teleskops (") α = 23 / Öffnung (Objektiv-/Spiegeldurchmesser in mm)

Spix zufolge müssen diese "theoretischen" Werte wegen atmosphärischer Turbulenzen in den meisten Nächten verdoppelt werden. Strukturen unter 0,16" (300 m) seien auch mit großen Teleskopen (größer als 10") praktisch nicht sichtbar.

Beispiel-Tabelle mit nach "Faustformeln" berechneten Auflösungen und verdoppelten Werten

			Theoretisch		Verdoppelt
Teleskop	Brennweite*	Öffnung	Krater	Rillen	Krater	Rillen
Refraktor	400...700	60	0,65"	0,38"	1,30"	0,76"
S-W Heritage 76	300	76	0,51"	0,30"	1,03"	0,61"
Refraktor	500...900	80	0,49"	0,29"	0,98"	0,58"
Meade ETX 90EC	1250	90	0,43"	0,26"	0,87"	0,51"
S-W Heritage 100P	400	100	0,39"	0,23"	0,78"	0,46"
S-W Skymax-102	1300	102	0,38"	0,23"	0,76"	0,45"
S-W Skymax-127	1500	127	0,31"	0,18"	0,61"	0,36"
S-W Explorer 150PDS	750	150	0,26"	0,15"	0,52"	0,31"
GSO GSD 680	1200	200	0,20"	0,12"	0,39"	0,23"
Meade Lightbridge 10"	1270	254	0,15"	0,09"	0,31"	0,18"

*) Ohne Bedeutung hier; 0,52" entsprechen etwa 1 km auf dem Mond.

Auflösung und Fotografie

Zur Abbildung einer bestimmten Auflösung benötigt man einen Sensor mit mindestens zwei bildaufnehmenden Pixeln auf dem der Auflösung entsprechenden Abstand. Dazu stellt man sich die Brennweite als Radius eines Kreises mit 360° vor, 1° wären dann 1/360 davon, 1' davon 1/60 und eine 1" davon wieder 1/60. Den Wert für eine Sekunde kann man dann mit dem tatsächlichen Auflösungswert in Sekunden multiplizieren, um den Abstand, der der Auflösung entspricht, zu bestimmen. Diesen kann man dann mit der Pixelgröße verwendeter oder anderer Sensoren vergleichen.

Beispiele:

Der Explorer 150PDS besitzt eine Brennweite von 750 mm. Das entspricht einem Kreisumfang von 4712 mm, 1 Grad = 13,1 mm, 1' = 0,22 mm, 1" = 0,0036 mm = 3,6 µm.
0,92" ist das Auflösungsvermögen des Teleskops und wird auf etwa 3,35 µm abgebildet. Zwei Pixel müßten also je 1,67µm groß sein, um mit einem Sensor das Auflösungsvermögen des Teleskops abbilden zu können.
Die Atik Infinity besitzt eine Pixelgröße von 6,4 µm und kann das Auflösungsvermögen des Teleskops nicht abbilden. Mit dem Sony-Sensor IMX224 (eVscope) mit einer Pixelgröße von 3,75 µm ist es auch nicht möglich. Mit dem Sony-Sensor IMX178 (im Stellina-Releskop und in der ZWO ASI178MC-Kamera), der eine Pixelgröße von 2,4 µm hat, wäre das vielleicht knapp der Fall...
Das eVscope besitzt eine Brennweite von 450 mm. Das entspricht einem Kreisumfang von 2827 mm, 1 Grad = 7,85 mm, 1' = 0,13 mm, 1" = 0,0022 mm = 2,2 µm.
1,21" ist das Auflösungsvermögen des Teleskops und wird auf 2,64 µm abgebildet. Zwei Pixel müßten also je 1,32 µm groß sein, um mit einem Sensor das Auflösungsvermögen des Teleskops abbilden zu können.
Mit keinem der Sensoren wird das Auflösungsvermögen des Teleskops also ausgeschöpft.
Das Stellina-Teleskop besitzt eine Brennweite von 400 mm. Das entspricht einem Kreisumfang von 2513 mm, 1 Grad = 6,98 mm, 1' = 0,116 mm, 1" = 0,0019 mm = 1,9 µm.
1,725" ist das Auflösungsvermögen des Teleskops und wird auf 3,34 µm abgebildet. Zwei Pixel müßten also je 1,7 µm groß sein, um mit einem Sensor das Auflösungsvermögen des Teleskops abbilden zu können.
Mit dem Sony-Sensor IMX178 (im Stellina-Teleskop und in der ZWO ASI178MC-Kamera) mit einer Pixelgröße von 2,4 µm könnte das vielleicht knapp erreicht werden...

Diese Abschätzungen orientieren sich an dem Artikel von Peter Oden Was ist eigentlich ... die Auflösung?. Es werden die Rayleigh-Auflösungen der Teleskope verwendet!

Menschliches Auge

Das menschliche Auge hat eine Auflösung von ca. 1' (in der Praxis, theoretisch ist es 20"). Für praktische astronomische Anwendungen werden aber oft 2' oder sogar 3' genannt.

(Nach: Was ist eigentlich ... die Auflösung? (Peter Oden, Abenteuer Astronomie) und Mathematik in der Astronomie (Teil 4): Das Auflösungsvermögen von Teleskopen (Stefan Gotthold, clearskyblog))

Auge-Okularabstand (Eye Relief)

Der Auge-Okularabstand (engl. eye relief) eines Teleskops, Mikroskops oder Fernglases ist der Abstand zwischen der äußersten Oberfläche des Okulars, den das Auge einnehmen kann, damit die Austrittspupille des Okulars noch der Eintrittspupille des Auges entspricht (übersetzt nach Wikipedia).

Der Wert des Auge-Okularabstandes ist besonders wichtig für Brillenträger, denn das Auge eines Brillenträgers ist typischerweise weiter vom Okular entfernt. Deshalb mus ein optisches Gerät für diese Nutzer einen größen Auge-Okularabstand erlauben, damit das gesamte Gesichtsfeld noch überblickt werden kann (übersetzt nach Wikipedia).

Austrittspupille

Bei optischen Geräten zur direkten visuellen Beobachtung – z. B. Teleskopen und Ferngläsern – wird als Austrittspupille (engl. exit pupil) oder Austrittsblende der Durchmesser des Strahlenbündels bezeichnet, der das Okular verlässt. (Nach Wikipedia)

Letztendlich bestimmt nur die Austrittspupille, wie hell das Bild eines bestimmten Objekts, zum Beispiel des Mondes, im Okular erscheint. Bei gleicher Austrittspupille erscheint es stets gleich hell, unabhängig von Teleskop, Öffnung und Vergrößerung.

Die Austrittspupille eines Teleskops sollte auf die Pupille, besser Eintrittspupille, des menschlichen Auges abgestimmt sein. Bei jungen Menschen ist die Pupille 7 mm und bei Erwachsenen etwa 6,4 mm groß nach Dunkeladaptation; mit zunehmendem Alter wird sie immer kleiner. Eine Austrittspupille von 4 mm ist geeignet und ausreichend für alle Beobachter.

Besitzt ein Okular eine zu große Austrittspupille, dann wird Licht vergeudet, das außerhalb der menschlichen Pupille auf das Auge trifft. Besitzt ein Okular eine zu kleine Austrittspupille, werden Beobachtungsobjekte zu dunkel (ab 1 mm für Galaxien und Nebel, ab 0,7 mm für Planeten, ab 0,5 mm für den Mond).

Nun noch zwei technische Anmerkungen:

Die Austrittspupille begrenzt zum Auge hin sowohl die minimale, als auch die maximale nutzbare Vergrößerung eines optischen Instruments.
Die Austrittspupille eines gegebenen Okulars (d.h. mit vorgegebener Brennweite) wird bei Teleskopen und Ferngläsern vom Öffnungsverhältnis (Brennweite/Objektivöffnung) des Instruments bestimmt (siehe Formeln).

Anwendungen für verschiedene Werte der Austrittspupille (Televue-Website, angepasst)

"Normalvergrößerung"

2 - 4 mm Austrittspupille: Erfahrungsgemäß werden diese Okulare am häufigsten verwendet.
4 - 3,5 mm Austrittspupille ist für die meisten großflächigen, flächenlichtschwachen Nebel optimal.
Mit 2 mm Austrittspupille nimmt das Auge bereits 80% der maximalen theoretischen Auflösung wahr; für viele Objekte ist die Wahrnehmbarkeit optimal, z.B. für die meisten Galaxien.

"Maximalvergrößerung"

1 mm (bis min. 0,8 - 0,5 mm) Austrittspupille: Mit 1 mm Austrittspupille nimmt man 95% der theoretisch maximal möglichen Auflösung wahr. Jede weitere Vergrößerung macht nur dann Sinn, wenn Teleskop und Augen gut sind.
0,8 mm Austrittspupille bringt bei perfektem Seeing die maximale Wahrnehmbarkeit kleiner, kontrastarmer Details, und ist die sinnvolle Maximalvergrößerung für Planeten.
0,5 mm Austrittspupille stellt die Maximalvergrößerung dar, jede weitere Vergrößerung bringt nichts mehr. Nutzbar sind 0,5 mm Austrittspupille nur zum Trennen enger Doppelsterne, und am äußersten Limit des Teleskops zur Wahrnehmung schwächster Details.

Azimutale (alt-azimutale) Montierung

Azimutale Montierungen, auch alt-azimutale Montierung oder Altazimut genannt, haben eine vertikale Hauptachse (Stehachse), um die sich die gesamte Anlage drehen kann. Das Beobachtungsinstrument selbst lässt sich um eine horizontale Achse zwischen Horizont und Zenit schwenken.

Diese Montierungen sind mechanisch einfacher und tragfähiger als andere Montierungen. Es muss aber in Kauf genommen werden, dass die Bewegungen um beide Achsen mit ständig veränderlichen Geschwindigkeiten erfolgen muss. Außerdem rotiert das Gesichtsfeld des Beobachtungsinstruments. Das heißt, für die Astrofotografie oder Messgeräte am Beobachtungsinstrument muss ebenfalls motorisch gedreht werden. Durch den Einsatz entsprechender Computertechnik können diese Steuerungsprobleme jedoch heute gelöst werden.

Die größten Teleskopanlagen haben azimutale Montierungen (wegen der größeren Tragfähigkeit). Dobson-Teleskope besitzen eine einfache azimutale (alt-azimutale) Montierung. (Aus: Wikipedia, angepaßt)

Beugungsscheibchen (Airy Disk)

Für Teleskope kann der Durchmesser des Beugungsscheibchens (engl. Airy disk) folgendermaßen berechnet werden:

D = 2,43932 * λ * (Öffnungsverhältnis des Teleskops) (D = Durchmesser des Beugungsscheibchens in mm; λ = Wellenlänge in mm, z.B. 546 nm = 0,000546 mm)

Beispiel: Mit einem Öffnungsverhältnis von F/4 und einer Wellenlänge von 546 nm erhalten wir einen Durchmesser von D = 0,00533 mm)

Der Durchmesser des Beugungsscheibchens errechnet sich in Winkelmaßen folgendermaßen:

A = 7200 * arctan (1,21966 * λ / d) (A = Durchmesser des Beugungsscheibchens in Bogensekunden, d = Durchmesser des Teleskop-Hauptspiegels in mm)

(Von: Oldham Optical UK, angepasst)

Deep Sky, Deep-Sky-Objekte

Unter dem Begriff Deep Sky (wörtlich: „tiefer Himmel“) werden in der Amateurastronomie diejenigen optisch beobachtbaren Himmelsobjekte zusammengefasst, die sich außerhalb des Sonnensystems befinden (also keine Asteroiden, Planeten oder Kometen), aber keine einzelnen Sterne sind. Zu ihnen zählen unter anderem alle Sternhaufen, Nebel und Galaxien.

Dem Begriff Deep Sky liegt keine Klassifizierung von Objekten bezüglich ihrer absoluten Entfernung zugrunde. Tatsächlich können Deep-Sky-Objekte relativ nah (Messier 45: 430 Lichtjahre) oder auch sehr weit entfernt sein (Messier 51: etwa 35 Mio. Lichtjahre).
(Von: Wikipedia)

Deklination

Die Deklination δ (vom Lateinischen für „Abweichung, Beugung“) ist eine der beiden Polarkoordinaten (Kugelkoordinaten) im rotierenden äquatorialen Koordinatensystem der sphärischen Astronomie. Dessen zweite Koordinate ist die Rektaszension. Man verwendet sie zur Positionsangabe von Himmelskörpern auf der gedachten Himmelssphäre.
(Von: Wikipedia)

Beim äquatorialen Koordinatensystem ist die Deklination δ der Erhebungs-Winkel über dem Himmelsäquator – womit sie der geografischen Breite φ nördlich bzw. südlich des Erdäquators entspricht (sie ist also das Analogon zur geographischen Länge, die sich auf die Erdkugel bezieht).

Die Werte von δ nördlich des Himmelsäquators werden positiv angegeben, südlich des Himmelsäquators negativ; die beiden Himmelspole haben +90° bzw. -90°.

Bild: Äquatoriales Koordinatensystem (Quelle: Wikipedia, ursprünglicher hochladender Benutzer: Sverdrup (veränderte das Original von Ulrich.fuchs), unter CC-Lizenz)

Siehe auch Äquatoriales Koordinatensystem

Dobson-Teleskop

Kurzform: Als Dobson-Teleskop bezeichnet man ein Gerät für astronomische Beobachtungen, das praktisch nur für Hobbyzwecke benutzt wird. In Fachkreisen auch kurz als „Dobson“ oder „Dob“ bezeichnet (englisch: dobsonian telescope). Es wurde von John Dobson Mitte der 1950er Jahre als besonders preisgünstiges Amateurfernrohr entwickelt.
(Von: Wikipedia)

Drei Mini-Dobsons von Sky-Watcher, beim rechten verkürzt ein Schiebemechanismus die Baulänge des Tubus

Gitterrohr-Dobson (10", Meade)

Volltubus-Dobson-Teleskop ( 8", GSO)

Langform: Ein Dobson-Teleskop ist ein Newton-Teleskop-Design mit sogenannter Alt-Azimut-Montierung. Das Design wurde von John Dobson Mitte der 50er Jahre entwickelt und in den 1960er Jahren von ihm populär gemacht. Die Konstruktion erlaubte es, die Größe von Teleskopen, die Amateurastronomen zur Verfügung standen, in beträchtlichem Ausmaß zu erhöhen. Dobson-Teleskope sind durch eine vereinfachte mechanische Konstruktion ausgezeichnet; diese ermöglicht es, ein großes, tragbares Teleskop mit geringem Aufwand aus leicht erhältlichen Komponenten preiswert herzustellen. Das Design ist für die visuelle Beobachtung schwacher Deep-Sky-Objekte wie Nebel und Galaxien optimiert. Diese Beobachtungsform erfordert einen großen Objektivdurchmesser (das heißt, eine große Lichtsammelleistung) bei relativ kurzer Brennweite und gute Tragbarkeit auf Reisen zu weniger "lichtverschmutzten" Orten.

Dobson-Teleskope sollen vor allem "Licht-Sammler" bei geringer Vergrößerung sein. Deshalb lässt das Design bestimmte Merkmale wie äquatoriales Tracking weg, die in anderen Amateurteleskopen zu finden sind. Dobson-Teleskope sind vor allem bei Amateur-Teleskopbauern beliebt. Bei diesen wurde das Design auch erstmals eingeführt, und dort entwickelt es sich ständig weiter. Eine Reihe kommerzieller Teleskop-Hersteller verkauft ebenfalls Teleskope, die auf diesem Entwurf basieren. Der Begriff "Dobson" wird momentan für eine ganze Reihe Newtonscher Reflektoren mit großer Öffnung (Apertur) verwendet, die einige der grundlegenden Dobson-Gestaltungsmerkmale verwenden, unabhängig von den Materialien, aus denen sie aufgebaut sind.
(Aus Wikipedia, frei übersetzt)

Eintrittspupille

Die Eintrittspupille (engl. entry pupil) ist eine tatsächliche oder scheinbare Öffnung, welche die in ein optisches System einfallenden Strahlenbündel begrenzt. Im Falle eines Teleskops mit einem Beobachter müssen wir sowohl die Eintrittspupille des Teleskops als auch die den menschlichen Auges betrachten.

Der Durchmesser der Eintrittspupille ist eine Kenngröße für die übertragene Leuchtdichte. Je nach Objektlage wird der Durchmesser der Eintrittspupille unterschiedlich berechnet.

Teleskope dienen zur Betrachtung von Objekte im Unendlichen. Hier wird direkt der Durchmesser (Hauptspiegel-Durchmesser bzw. Objektivöffnung) als Kenngröße angegeben. Oft wird statt des Hauptspiegel-Durchmessers die Objektivöffnung angegeben, denn der Hauptspiegel-Durchmesser kann nämlich durch bestimmte Baumerkmale des Teleskops unter Umständen nicht voll genutzt werden. Vereinfacht gesamt, sammelt ein Teleskop umso mehr Licht, je größer seine Eintrittspupille (also der Hauptspiegel-Durchmesser bzw. die Objektivöffnung) ist.

Nun zum Beobachter! Die Pupille, besser Eintrittspupille, des menschlichen Auges ist bei jungen Menschen 7 mm und bei Erwachsenen etwa 6,4 mm groß nach Dunkeladaptation; mit zunehmendem Alter wird sie immer kleiner. Dies bei der Wahl der Austrittspupille von Teleskopen berücksichtigt werden. Eine Austrittspupille von 4 mm ist geeignet und ausreichend für alle Beobachter.

Ekliptik

Von der Erde aus gesehen scheint sich die Sonne gegenüber den Hintergrundsternen zu bewegen. Die Ekliptik ist die von der Erde aus gesehene scheinbare Bahn der Sonne vor dem Fixsternhintergrund im Laufe eines Jahres. Sie resultiert aus dem Umlauf der Erde um die Sonne, der sich nach 365 Tagen wiederholt.

Die Ekliptik bildet auf der Himmelskugel einen Großkreis. Dieser definiert eine Ebene, die Ekliptikebene oder Ekliptikalebene. Die Ekliptikebene schneidet die vom Himmelsäquator definierte Äquatorebene unter einem Winkel, der als Schiefe der Ekliptik oder auch Erdneigung bezeichnet wird und derzeit etwa 23,4° beträgt. Die Schnittpunkte der Ekliptik mit der Äquatorebene sind der Frühlings- und der Herbstpunkt, die Punkte, an denen sich die Sonne zu den Zeitpunkten der Tagundnachtgleichen befindet.
(Von: Wikipedia, angepasst)

Bild: Äquatoriales Koordinatensystem (Quelle: Wikipedia, ursprünglicher hochladender Benutzer: Sverdrup (veränderte das Original von Ulrich.fuchs), unter CC-Lizenz)

Himmelsäquator

Der Himmelsäquator ist der Großkreis auf der gedachten Himmelskugel, auf dem sie von der Ebene des Erdäquators geschnitten wird. Anders ausgedrückt: Wenn man in den Mittelpunkt einer gläsernen Erdkugel eine Glühlampe stellen würde, ist der Himmelsäquator gerade die Projektion des Erdäquators an die scheinbare Himmelskugel. Er teilt die Himmelskugel in eine Nord- und eine Südhälfte.

Da die Erdachse gegenüber der Ebene des Sonnensystems geneigt ist, schneidet der Himmelsäquator die Ekliptik – die scheinbare Ebene der Umlaufbahn der Sonne um die Erde – derzeit unter einem Winkel von 23,4° (Schiefe der Ekliptik). Die beiden Schnittpunkte werden als Frühlingspunkt bzw. Herbstpunkt bezeichnet, da sich in ihnen die Projektion der Sonne an die scheinbare Himmelskugel zu den Tag-und-Nacht-Gleichen (auch: Tagundnachtgleichen) im Frühling bzw. Herbst befindet.
(Aus: Wikipedia (Himmelsäquator), angepasst)

Bild: Äquatoriales Koordinatensystem (Quelle: Wikipedia, ursprünglicher hochladender Benutzer: Sverdrup (veränderte das Original von Ulrich.fuchs), unter CC-Lizenz)

Himmelspole

Definitionen:

Die Himmelspole werden definiert, indem die geografischen Pole der Erde gedanklich zum Himmel verlängert werden. Der Punkt, an dem die Polachse die scheinbare Himmelskugel durchstoßen würde, ist der Himmelsnord- bzw. Südpol. (Aus: www.hobby-astronomie.com).
Als Himmelspole werden die Durchstoßpunkte der Erdachse mit der Himmelskugel bezeichnet. (Aus: Wikipedia, angepasst)

Der Himmelsnordpol ist jener Punkt nahe dem Polarstern (α Ursae minoris) im Sternbild Kleiner Bär (bzw. Kleiner Wagen), um den sich scheinbar das Himmelsgewölbe in seiner täglichen Bewegung dreht; der Himmelssüdpol liegt ihm gegenüber, in seiner Nähe liegt aber nur ein schwacher Stern, σ Octantis.

Der Himmelspol ist – auf längere Zeitspannen gesehen – nicht stabil. Einerseits verschiebt sich die Erdachse infolge der Präzession in knapp 26.000 Jahren entlang eines großen Kegels um den Pol der Ekliptik, andererseits schwankt ihr Durchstoßpunkt mit der Erdoberfläche um etwa 10 Meter.
(Aus: Wikipedia, angepasst)

Bild: Äquatoriales Koordinatensystem mit Himmels-Nordpol (Quelle: Wikipedia, ursprünglicher hochladender Benutzer: Geof, unter CC-Lizenz)

Lichtsammelleistung

Die Lichtsammelleistung eines Teleskops wird als Vielfaches der Lichtsammelleistung des menschlichen Auges angegeben:

Lichtsammelleistung = (Öffnung in mm)² / 49

(Die maximale Öffnung des menschlichen Auges ist etwa 7 mm)

Montierung

Eine Montierung (oder Plattform) ist eine Einrichtung, die in der praktischen Astronomie folgende Aufgaben erfüllen soll:

ein astronomisches Beobachtungsinstrument (meist ein Teleskop oder eine Kamera) zu tragen und es auf ein gewünschtes Himmelsobjekt zu richten
die Erddrehung zu kompensieren. Die Nachführung des Beobachtungsinstruments kann von Hand oder durch einen motorischen Antrieb erfolgen. Das Beobachtungsinstrument bleibt so über einen beliebig langen Zeitraum auf bestimmte Koordinaten des Sternhintergrundes gerichtet
Beobachtungsobjekte, die sich relativ zum Sternhintergrund merklich bewegen, genau zu verfolgen. Dies betrifft Kometen, Planetoiden und Erdsatelliten, kaum hingegen Mond und Planeten. Hierzu muss die Montierung über weitere Antriebe, eventuell auch Achsen verfügen. Die erforderlichen Daten für die Computersteuerung kommen aus einem Programm zur Bahnbestimmung.

(Von: Wikipedia)

Populäre Montierungen sind:

Altazimutale oder alt-azimutale Montierung
Parallaktische (äquatoriale) Montierung

Newton-Teleskop/-Reflektor

Das Newton-Teleskop (oder der Newton-Reflektor) wurde vom britischen Wissenschaftler Sir Isaac Newton (1642-1727) erfunden und ist eine Form des Spiegelteleskops, die einen konkaven Primärspiegel und einen flachen diagonalen Sekundärspiegel verwendet. Newtons erstes Spiegelteleskop wurde im Jahre 1668 fertig gestellt und ist das früheste bekannte funktionierende Spiegelteleskop. Wegen seines einfachen Designs ist das Newton-Teleskop bei Herstellern von Amateur-Teleskopen sehr beliebt. (Von: Wikipedia, übersetzt)

Öffnung (Apertur)

Mit Öffnung wird der Durchmesser des Lichteinlasses eines Teleskops angegeben (Apertur). Beim Spiegelteleskop ist dies der Durchmesser des Hauptspiegels oder ein Wert, der berücksichtigt, dass der Hauptspiegel-Durchmesser durch bestimmte Baumerkmale des Teleskops nicht voll genutzt werden kann.

Öffnungsverhältnis

Das Öffnungsverhältnis eines Teleskops ergibt sich aus Teleskop-Brennweite und der Öffnung (Hauptspiegel- oder Objektiv-Durchmesser):

Öffnungsverhältnis = (Brennweite des Teleskops) / (Öffnung des Teleskops)

Parallaktische (Äquatoriale) Montierung

Die parallaktische Montierung, auch äquatoriale Montierung genannt, ist eine Einrichtung zur Halterung und Bewegung eines Teleskops, bei der, im Gegensatz zu anderen Montierungstypen, eine der Achsen genau parallel zur Erdachse ausgerichtet ist. (Von: Wikipedia)

Bei astronomischen Teleskop-Montierungen ist die äquatoriale Achse mit einer zweiten senkrechten Bewegungsachse gepaart. Die äquatoriale Achse der Montierung ist oft mit einem motorisierten Antrieb versehen, der diese Achse alle 23 Stunden und 56 Minuten synchron mit der scheinbaren täglichen Bewegung des Himmels genau einmal dreht. Äquatorial-Montierungen unterscheiden sich damit von den mechanisch einfacheren altazimutalen Montierungen, die für beide Achsen Bewegungen mit variabler Drehzahl benötigen, um einem festen Gegenstand am Himmel verfolgen zu können.

Äquatorial-Montierungen gibt es in vielen Formen. In den letzten zwanzig Jahren wurde das motorisierte Verfolgen (Tracking) von Himmelskörpern zunehmend um eine computerisierte Objektlokalisierung ergänzt. Hierbei gibt es zwei Haupttypen. Beim ersten Typus überwacht der Computer die Position des Teleskops am den Himmel, und der Bediener muss das Teleskop bewegen. Go-to-Systeme verwenden (in den meisten Fällen) Servomotoren, und der Bediener braucht das Instrument nicht mehr zu berühren, um dessen Position am Himmel zu ändern. Die Computer befinden sich typischerweise entweder in einem Handsteuergerät, oder ein gesonderter Laptop-Computer, der auch zum Erfassen von Bildern einer elektronischen Kamera verwendet werden kann, übernimmt die Steuerungsfunktion. Moderne Teleskopsysteme besitzen oft eine elektrische Schnittstelle für "Autoguiding".

Bei neuen Teleskop-Designs für große professionelle Anwendungen sind parallaktische Montierungen seit Jahrzehnten in Ungnade gefallen. Aber auf der Amateur-Ebene sind sie, vor allem für die Astrofotografie, nach wie vor beliebt.
(Aus: Wikipedia, übersetzt und angepaßt)

Rektaszension

Die Rektaszension α oder a (lat. ascensio recta = gerader Aufstieg) ist eine der beiden Polarkoordinaten im rotierenden äquatorialen Koordinatensystem der sphärischen Astronomie. Dessen zweite Koordinate ist die Deklination. Man verwendet sie zur Positionsangabe von Himmelskörpern auf der gedachten Himmelssphäre.

Die Rektaszension ist der auf den Himmelsäquator bezogene Winkel zwischen dem Frühlingspunkt und dem Längenkreis, auf dem der beobachtete Himmelskörper steht. Sie ist das Analogon zur geographischen Länge, die sich auf die Erdkugel bezieht.

Die Rektaszension wird häufiger im Zeitmaß als in Grad oder Bogenmaß angegeben. Die Angabe im Zeitmaß nimmt Bezug darauf, dass die scheinbare Rotation der Sterne um die Erde proportional zur Zeit ist und Zeitdifferenzen einfacher als Winkel bestimmt werden können. Wenn ein Stern z.B. am Äquator eine Stern-Stunde nach dem Frühlingspunkt aufgeht, so hat er die Rektaszension 15° (in einem Stern-Tag zu 24 Stern-Stunden bewegen sich die Sterne nämlich scheinbar auf einem vollen Kreis mit 360°).
(Von: Wikipedia)

Bild: Äquatoriales Koordinatensystem (Quelle: Wikipedia, ursprünglicher hochladender Benutzer: Sverdrup (veränderte das Original von Ulrich.fuchs), unter CC-Lizenz)

Siehe auch Äquatoriales Koordinatensystem

Seeing

Unter Seeing versteht man die Luftunruhe, hauptsächlich in der bodennahen Luftschicht, aber auch in der Teleskopkuppel und ihrer direkten Umgebung, die man mit bloßem Auge als das Flimmern der Sterne wahrnimmt. Je stärker die Sterne flimmern, desto schlechter ist das Seeing.

Bei visueller Beobachtung im Teleskop äußert sich das Seeing durch rasches Hin- und Hertanzen des Sterns im Bruchteil von Sekunden, bei manchen Wetterbedingungen auch durch ein verschwommenes Bild. In der Astrofotografie vergrößert es das fast punktförmige Sternscheibchen je nach Dauer der Belichtungszeit.

Das Seeing wirkt sich negativ auf die Auflösung und Schärfe von visuellen Beobachtungen und Astrofotos aus, indem bei schlechtem Seeing feine Details an Sonne, Mond und Planeten verschmiert werden. Folglich wird auch die maximal sinnvolle Vergrößerung durch das Seeing mitbestimmt: Je schlechter das Seeing ist, umso schwächer kann vergrößert werden. In Nächten mit schlechtem Seeing kann es daher völlig unmöglich sein, visuell und fotografisch scharfe Bilder zu erhalten. Dies trifft jedoch nur auf fein strukturierte Objekte wie Sonne, Mond, Planeten und Doppelsterne zu.

Als Seeing wird auch das Maß der Bildunschärfe durch Luftunruhe bezeichnet. Es wird normalerweise in Bogensekunden angegeben und dabei oft über die Halbwertsbreite FWHM (Full width at half maximum) der Abbildung einer Punktquelle (z. B. ein entfernter Stern) gemessen.
(Von: www.hobby-astronomie.com, angepasst; Wikipedia: Seeing, angepasst)

Sehwinkel (Gesichtsfeld)

Der scheinbare Sehwinkel (scheinbares Gesichtsfeld) ist ein Maß für den Winkel, den ein Okular als Himmelsausschnitt zeigt. Er hängt von der Bauart des Okulars ab und wird üblicherweise vom Hersteller angegeben. Beispiele:

Kellner-Okular: 42°
Plössl-Okular: 52-55°
Planeten-Okular (HR Planetary): 58 - 60°
Okular mit "optimalem" Sehwinkel (Weitwinkel-Okular): 68 - 70° (so werden diese Okulare beworben...)
Super-Weitwinkel-Okular, Nagler-Okular: 80 - 82°
Ethos-Okular und andere ??? Okulare: 100 - 110°

Okularen bis 55° wird gern ein "Tunnel-Blick" bescheinigt. Okulare mit 80° und mehr werden gern damit beworben, dass man "vor den Objekten im Weltraum zu schweben scheint". Okulare um 70° gelten als "ideal für das menschliche Auge" und als "optimal für die Beobachtung" - bei größeren Gesichtfeldern muss man "um die Ecke gucken", um das ganze Gesichtsfeld übersehen zu können. Mehr über Okular-Bautypen findet sich bei Wikipedia.

Hinweis: Sky-Watcher gibt 42° als allgemein gültigen Wert für den scheinbaren Sehwinkel der meisten Amateur-Okulare an. Damit sind dann wohl Kellner-Okulare gemeint.

Der wahre Sehwinkel ist ein Maß für die Größe der Objekte, die im Teleskop beobachtet werden können:

Wahrer Sehwinkel = (Scheinbarer Sehwinkel) / Vergrößerung = (Scheinbarer Sehwinkel) * (Brennweite des Okulars) / (Brennweite des Teleskops)

Er ergibt sich also, indem man den scheinbaren Sehwinkel durch die Vergrößerung teilt (z.B.: 70 Grad / 100 = 0,7 Grad).

Beispiel: Der Mond entspricht einem Sehwinkel von etwa 0,5° (die Sonne ebenfalls, deshalb gibt es totale Sonnenfinsternisse).

Vergrößerung

Die Vergrößerung eines Teleskops errechnet sich aus Brennweite des Teleskops und des Okulars:

Vergrößerung = (Brennweite des Teleskops) / (Brennweite des Okulars)

Sie hängt also bei vorgegebenem Teleskop allein von der Okularbrennweite ab und kann schnell im Kopf ermittelt werden. In der Praxis ist es wichtig zu wissen, für welche Aufgaben sich welche Vergrößerung eignet. Ich habe folgende Empfehlungen für den Einsatz von Vergrößerungen gefunden:

Ganz niedrig (10-20 x): Aufsuchen von Objekten, ausgedehnte Objekte (großflächige Nebel, Andromeda-Galaxie, ...) (von mir ergänzt)
Niedrig (30-50 x): Sternhaufen, Galaxien und Nebel
Mittel (80-100 x): Krater und Täler auf dem Mond, Saturnringe, Jupiter und seine Monde
Hoch (150-200 x; mit meinem Heritage 100P-Teleskop praktisch nicht möglich): Bergspitzen und feinere Details auf dem Mond, Oberflächendetails des Mars, Trennung nahe beieinander stehender Doppelsterne

Maximal (sinnvoll) nutzbare Vergrößerung, Förderliche Vergrößerung

Die maximal (sinnvoll) nutzbare Vergrößerung eines Teleskops ist dadurch definiert, dass die Auflösung des Teleskops und des Auges genau aufeinander abgestimmt sind. Sie ist die höchste Vergrößerung, bei der noch ein Gewinn an Details gegeben ist. Erst bei dieser Vergrößerung schöpft man die Auflösung und die Lichtsammelleistung des Teleskops voll aus und erreicht dessen stellare Grenzgröße. Darüber hinaus werden keine weiteren Details mehr sichtbar und man spricht von "leerer Vergrößerung". Übrigens ist die Austrittspupille bei dieser Vergrößerung genau 0,5 mm groß. Die maximal (sinnvoll) nutzbare Vergrößerung hängt im wesentlichen von der Öffnung des Teleskops ab (Hauptspiegel-Durchmesser oder Objektivöffnung) ab:

Maximal nutzbare Vergrößerung = (Öffnung des Teleskops in mm) * X

X beträgt:

1,5 für Newton Newton Spiegelteleskope (einschließlich Dobsons), Rich Field Refraktoren, Schmidt Cassegrains
2 für Refraktoren ab f/8, Maksutov-Teleskope

Die Austrittspupille hat bei dieser Vergrößerung und X = 2 eine Größe von 0, 5 mm und bei X = 1.5 von 0,67 mm.

Förderliche Vergrößerung

Stoyan (Deep Sky Reiseführer) spricht von der "förderlichen" Vergrößerung, bei der die maximale Grenzgröße im Teleskop erreicht wird und bei der das Beugungsscheibchen (Airy Disk) gerade nicht aufgelöst wird. Sie errechnet sich zu:

Förderliche Vergrößerung = Öffnung / 0,7

Das entspricht ungefähr einem Faktor X von 1,5 (genau: 1,43) in der ersten Formel.

Für kleinere flächige Deep-Sky-Objekte hält Stoyan (Deep Sky Reiseführer) es für sinnvoll, weit über die förderliche Vergrößerung hinaus bis zur Maximalvergrößerung zu gehen.

Maximalvergrößerung

Für kleinere flächige Deep-Sky-Objekte hält Stoyan (Deep Sky Reiseführer) es für sinnvoll, weit über die förderliche Vergrößerung hinaus bis zur Maximalvergrößerung zu gehen, die zweimal so hoch ist wie die förderliche Vergrößerung (also etwa Faktor X = 3). Anhängig von der Bauart des Teleskops und der Luftunruhe (Seeing), können diese höheren Vergrößerungen aber nicht immer erreicht werden. Kleinere Teleskope erreichen ihre Maximalvergrößerung leichter, weil sie niedriger ist als die von großen Teleskopen und so das Seeing weniger stört.

Minimalvergrößerung

Die minimal (sinnvoll) nutzbare Vergrößerung ist folgendermaßen definiert: Austrittspupille des Teleskops und Augenpupille sind gleich groß, es geht also kein Licht verloren. Je nach Quelle werden Werte zwischen 5 mm und 8mm für die Augenpupille angesetzt. Typischerweise werden jedoch 7 mm oder 6,5 mm bei der Berechnung der Minimalvergrößerung verwendet.

Die minimal (sinnvoll) nutzbare Vergrößerung/Normalvergrößerung wird direkt oder indirekt durch die Austrittspupille bestimmt:

Minimal nutzbare Vergrößerung = (Brennweite des Teleskops) / (Maximal nutzbare Okularbrennweite) = (Brennweite des Teleskops) / (Öffnungsverhältnis * Austrittspupille) = (Öffnung des Teleskops) / (Austrittspupille)

Bei zu geringer Vergrößerung (z.B. bedingt durch eine zu lange Okularbrennweite) wird das aus dem Okular austretende Licht nicht mehr vollständig vom Auge genutzt (die Austrittspupille ist zu groß).