Quick & Dirty Astronomy Glossary

Introductory Notes | Glossary | References

On this page, I collect some useful definitions of astronomy terms in a small glossary, plus a few links. With respect to telescopes, I focus on Dobsonian telescopes.

Overview of Terms

Italic: In preparation

Note: See also page Telescope Calculations for more information, formulae, and examples.

 

Introductory Notes

The following glossary is not intended to be complete by any means, because there are so many useful information sources on the Internet. The glossary definitions that I provide here are related to the telescopes that I describe on this site and may be useful for understanding their characteristics.

 

Glossary

Airy Disk

The airy disk (or Airy disk after its discoverer) is the size of the disk into which a light point is expanded through diffraction. For telescopes, the diameter of the airy disk can be calculated as follows:

Example: If focal ratio = F/4 and a wavelength of 546 nm used, then D = 0.00533 mm)

Another formula for the diameter of the airy disc is:

(From Oldham Optical UK, adapted)

Rules of Thumb

The diameter of the Airy disk, which is the effective aperture diameter of an optical system, determines its resolving power. Two points can be separated reliably according to the Rayleigh criterion if the maxima of their images are separated by at least the radius of the Airy disk. The diameter also indicates the minimum size with which stars are imaged in the telescope.

The diameter D (length, angular size) of the Airy disk is calculated according to the following "rules of thumb" (for the exact formulas see the appendix):

Often only the rounded value "277" is used. In angular measure, the Airy disk is twice as large as the Rayleigh resolving power (on which it is based), because the resolving power refers to the radius, while the Airy disk is typically used with the diameter.

Altazimuth (Alt-Azimuth) Mount

An altazimuth or alt-azimuth mount is a simple two-axis mount for supporting and rotating an instrument about two mutually perpendicular axes – one vertical and the other horizontal. Rotation about the vertical axis varies the azimuth (compass bearing) of the pointing direction of the instrument. Rotation about the horizontal axis varies the altitude (angle of elevation) of the pointing direction.

When used as an astronomical telescope mount, the biggest advantage of an alt-azimuth mount is the simplicity of its mechanical design. The primary disadvantage is its inability to follow astronomical objects in the night sky as the Earth spins on its axis the way that an equatorial mount can. Equatorial mounts only need to be rotated about a single axis, at a constant rate, to follow the rotation of the night sky (diurnal motion). Altazimuth mounts need to be rotated about both axes at variable rates, achieved via microprocessor based two-axis drive systems, to track equatorial motion. This imparts an uneven rotation to the field of view that also has to be corrected via a microprocessor based counter rotation system. On smaller telescopes an equatorial platform is sometimes used to add a third "polar axis" to overcome these problems, providing an hour or more of motion in the direction of right ascension to allow for astronomical tracking. The design also does not allow for the use of mechanical setting circles to locate astronomical objects although modern digital setting circles have removed this shortcoming. (From Wikipedia)

Dobsonian telescopes have an altazimuth (alt-azimuth) mount.

Aperture

The term aperture refers to the diameter of the opening of a telescope. For mirror telescopes this is either the diameter of the primary mirror or a value that takes care of obstructions that limit the light receiving area.

Celestial Equator

The celestial equator is a great circle on the imaginary celestial sphere, in the same plane as the Earth's equator. In other words, it is a projection of the terrestrial equator out into space. As a result of the Earth's axial tilt, the celestial equator is inclined by 23.4° with respect to the ecliptic plane.
(From Wikipedia, adapted)

Celestial Pole

The north and south celestial poles are the two imaginary points in the sky where the Earth's axis of rotation, indefinitely extended, intersects the celestial sphere. The north and south celestial poles appear permanently directly overhead to an observer at the Earth's North Pole and South Pole respectively. As the Earth spins on its axis, the two celestial poles remain fixed in the sky, and all other points appear to rotate around them, completing one circuit per day (strictly per sidereal day).

The celestial poles do not remain permanently fixed against the background of the stars. Because of a phenomenon known as the precession of the equinoxes, the poles trace out circles on the celestial sphere, with a period of about 25,700 years.
(From: Wikipedia, adapted)

Declination

In astronomy, declination (abbreviated dec; symbol δ) is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle or right ascension. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question.
(From: Wikipedia)

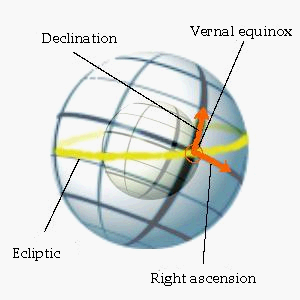
Figure: Equatorial coordinate system (Source: Wikipedia, original uploader: Sverdrup (changed the original by Ulrich.fuchs), under CC license)

See also Equatorial Coordinate System

Deep-Sky Object

Deep-sky objects are astronomical objects other than individual stars and Solar System objects (such as Sun, Moon, planets, comets, etc.). The classification is used for the most part by amateur astronomers to denote visually observed faint naked eye and telescopic objects such as star clusters, nebulae and galaxies.
(From: Wikipedia)

Dobsonian Telescope

A Dobsonian telescope is an alt-azimuth mounted Newtonian telescope design popularized by John Dobson starting in the 1960s credited with vastly increasing the size of telescopes available to amateur astronomers. Dobson's telescopes featured a simplified mechanical design that was easy to manufacture from readily available components to create a large, portable, low-cost telescope. The design is optimized for visually observing faint deep sky objects such as nebulae. This type of observation requires a large objective diameter (i.e. light-gathering power) of relatively short focal length and portability for travel to relatively less light polluted locations.

Three Mini Dobson telescopes (Sky-Watcher); the right telescope can be made smaller for easier storage and transportation

Truss-tube Dobson (10", Meade)

Full-tube Dobson telescope (8", GSO)

Dobsonians are intended to be what is commonly called a "light bucket" operating at low magnification, and therefore the design omits features found in other amateur telescopes such as equatorial tracking. Dobsonians are popular in the amateur telescope making community, where the design was pioneered and continues to evolve. A number of commercial telescope makers also sell telescopes based on this design. The term "Dobsonian" is currently used for a whole range of large-aperture Newtonian reflectors that use some of the basic Dobsonian design characteristics, regardless of the materials from which they are constructed.
(From Wikipedia)

Ecliptic

The ecliptic is the apparent path of the Sun on the celestial sphere, and is the basis for the ecliptic coordinate system. It also refers to the plane of this path, which is coplanar with the orbit of Earth around the Sun (and hence the apparent orbit of the Sun around Earth). The path of the Sun is not normally noticeable from Earth's surface because Earth rotates, carrying the observer through the cycles of sunrise and sunset, obscuring the apparent motion of the Sun with respect to the stars.

Because Earth's rotational axis is not perpendicular to its orbital plane, Earth's equatorial plane is not coplanar with the ecliptic plane, but is inclined to it by an angle of about 23.4°, which is known as the obliquity of the ecliptic. (From Wikipedia)

Figure: Equatorial coordinate system (Source: Wikipedia, original uploader: Sverdrup (changed the original by Ulrich.fuchs), under CC license)

Equatorial Coordinate System

The equatorial coordinate system is a widely used celestial coordinate system used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the center of the Earth, a fundamental plane consisting of the projection of the Earth's equator onto the celestial sphere (forming the celestial equator), a primary direction towards the vernal equinox, and a right-handed convention.

The equatorial coordinate system in spherical coordinates:

The fundamental plane is formed by projection of the Earth's equator onto the celestial sphere, forming the celestial equator. The primary direction is established by projecting the Earth's orbit onto the celestial sphere, forming the ecliptic, and setting up the ascending node of the ecliptic on the celestial equator, the vernal equinox. Right ascensions are measured eastward along the celestial equator from the equinox, and declinations are measured positive northward from the celestial equator. Projections of the Earth's north and south geographic poles form the north and south celestial poles, respectively (a right-handed convention means that coordinates are positive toward the north and toward the east in the fundamental plane). (From Wikipedia, adapted)

Figure: Equatorial coordinate system (Source: Wikipedia, original uploader: Sverdrup (changed the original by Ulrich.fuchs), under CC license)

Equatorial Mount

An equatorial mount (or platform) is a mount for instruments that follows the rotation of the sky (celestial sphere) by having one rotational axis parallel to the Earth's axis of rotation. This type of mount is used for astronomical telescopes and cameras. The advantage of an equatorial mount lies in its ability to allow the instrument attached to it to stay fixed on any object in the sky that has a diurnal motion by driving one axis at a constant speed. Such an arrangement is called a sidereal drive.

In astronomical telescope mounts, the equatorial axis (the right ascension) is paired with a second perpendicular axis of motion (known as the declination). The equatorial axis of the mount is often equipped with a motorized "clock drive", that rotates that axis one revolution every 23 hours and 56 minutes in exact sync with the apparent diurnal motion of the sky. They may also be equipped with setting circles to allow for the location of objects by their celestial coordinates. Equatorial mounts differ from mechanically simpler altazimuth mounts, which require variable speed motion around both axes to track a fixed object in the sky. Also, for astrophotography, the image does not rotate in the focal plane, as occurs with altazimuth mounts when they are guided to track the target's motion, unless a rotating erector prism or other field-derotator is installed.

Equatorial telescope mounts come in many designs. In the last twenty years motorized tracking has increasingly been supplemented with computerized object location. There are two main types. Digital setting circles take a small computer with an object database that is attached to encoders. The computer monitors the telescope's position in the sky. The operator must push the telescope. Go-to systems use (in most cases) servo motors and the operator need not touch the instrument at all to change its position in the sky. The computers in these systems are typically either hand-held in a control "paddle" or supplied through an adjacent laptop computer which is also used to capture images from an electronic camera. The electronics of modern telescope systems often include a port for autoguiding.

In new observatory designs, equatorial mounts have been out of favor for decades in large-scale professional applications. At the amateur level, however, equatorial mounts remain popular, particularly for astrophotography.
(From Wikipedia, adapted)

EQ Platform (Equatorial Platform, Tracking Platform)

Dobsonians are alt-azimuthal telescopes and therefore, tracking of sky objects at higher magnifications is getting hard. EQ platforms (equatorial platforms, tracking platforms), proposed by Adrien Poncet in 1977 and further refined since then by many others, solve this problem. An EQ platform serves as an equatorially mounted table for the telescope, which is used instead of the ground board. An EQ platform maintains the intuitively simple handling of the Dobsonian telescope.

An EQ platform automatically tracks sky objects usually for about an hour, then it must be reset. It is powered by a simple electric motor, which is usually powered by a 9V battery.
(After Reiner Vogel, adapted)

Link:

Eye Relief

Short: Eye relief is defined as the distance a binocular or spotting scope can be held away from the eye and still presents the full field of view. (From deu.proz.com/kudoz/english_to_german/physics/2699015-eye_relief.html)

Wikipedia: The eye relief of a telescope, a microscope, or binoculars is the distance from the last surface of an eyepiece at which the eye can be placed to match the eyepiece exit pupil to the eye's entrance pupil. Short eye relief requires the observer to press his or her eye close to the eyepiece in order to see an unvignetted image. An exit pupil larger than the observer's pupil wastes some light, but allows for movement between eye and eyepiece without vignetting. Conversely, an exit pupil smaller than the eye's pupil results in a vignetted image. The optical designer must also consider that the pupil of the human eye varies in size with lighting conditions and the age of the observer.

Eye relief can be particularly important for eyeglass wearers and shooters. The eye of an eyeglass wearer is typically further from the eyepiece which necessitates a longer eye relief in order to still see the entire field of view. (From Wikipedia)

Exit Pupil (and Entrance Pupil)

In optics, the exit pupil is a virtual aperture in an optical system. Only rays which pass through this virtual aperture can exit the system. The exit pupil is the image of the aperture stop in the optics that follow it. In a telescope or compound microscope, this image is the image of the objective element(s) as produced by the eyepiece. The size and shape of this disc is crucial to the instrument's performance, because the observer's eye can see light only if it passes through this tiny aperture.

To use an optical instrument, the entrance pupil of the viewer's eye must be aligned with and be of similar size to the instrument's exit pupil. This properly couples the optical system to the eye and avoids vignetting. (The entrance pupil of the eye is the image of the anatomical pupil as seen through the cornea.) The location of the exit pupil thus determines the eye relief of an eyepiece. Good eyepiece designs produce an exit pupil of diameter approximating the eye's apparent pupil diameter, and located about 20 mm away from the last surface of the eyepiece for the viewer's comfort. If the disc is much larger than the eye's pupil, much of the light will be lost instead of entering the eye; if smaller, the view will be vignetted. If the disc is too close to the last surface of the eyepiece, the eye will have to be uncomfortably close for viewing; if too far away, the observer will have difficulty maintaining the eye's alignment with the disc.

For a telescope, the diameter of the exit pupil can be calculated by dividing the focal length of the eyepiece by the focal ratio (f-number) of the telescope. More simply, it is the diameter of the objective lens divided by the magnification (see calculations).

The exit pupil determines in the direction of the eye the minimum as well as the maximum usable magnification of an optical instrument. (From Wikipedia)

After dark adaptation, the pupil is about 7 mm wide for young people and about 6.4 mm wide for adults; it gets smaller with growing age. An exit pupil of 4 mm is suitable and sufficient for observers of all ages. If the exit pupil of an eyepiece is larger than the observer's pupil, light is wasted that falls outside of the human pupil. If the exit pupil of an eyepiece is too small, objects become too dim (below 1 mm for deep sky objects, below 0.7 mm for planets, below 0.5 mm for the moon).

Uses for different Values of the Exit Pupil (Televue Website, adapted and translated)

"Normal Magnification"

"Maximum Magnification"

Field of View

The apparent field of view (viewing angle) determines the angle that is shown by an eyepiece as a section of the sky. It depends on the type of the eyepiece an is usually given by the manufacturer of the eyepiece. Here are some examples:

Eyepieces with a field of view up to 55° are often characterized as providing "tunnel vision." Eyepieces with a field of view of 80° and more are often advertised as that you are "floating in front of objects in space." Eyepieces with a viewing angle around 70° are considered as "ideal for the human eye" and as "optimal for observation" - with larger fields of view you have to "look around the corner" to overlook the whole field of view. More about eyepiece types can be found on Wikipedia.

Note: Sky-Watcher lists 42° as a suitable value for most amateur eyepieces. This seems to refer to Kellner eyepieces.

The true field of view determines the size of objects that can be observed in a telescope

Example: The moon corresponds to a field of view of about 0.5° (the sun as well; that's why we can have total eclipses of the sun)

Focal Ratio

The focal ratio of a telescope is given by the ration of the focal length of the telescope and the aperture (diameter of the primary mirror of objective):

Light Gathering Power

The light gathering power of a telescope is expressed in multiples of the light gathering power of the human eye:

(The maximum aperture of the naked eye is about 7 mm)

Magnification (Visual Power)

The magnification of a telescope is calculated from the ratio of the focal length of the telescope and the focal length of the eyepiece:

For a given telescope, magnification depends solely on the focal length of the eyepiece and can be easily calculated in your head. In practice, it is important to know, which magnification serves which purpose. I found the following recommendations for the use of magnifications:

Maximum Useful Magnification

The maximum practical visual power / useful magnification of a telescope is defined by the fact that the resolutions of the telescope and the eye match. It is the highest magnification at which there is still a gain in detail. Beyond that no further details become visible and one speaks of an "empty magnification." The maximum practical visual power / useful magnification is more or less determined by the aperture of the telescope (diameter of the primary mirror or objective):

X amounts to:

The exit pupil has a size of 0.5 mm at this magnification for X = 2, and of 0.67 mm for X = 1.5.

"Beneficial" visual power

Stoyan (Deep Sky Reiseführer) speaks of the "beneficial" visual power, at which the airy disk is still not resolved and at which the magnitude limit of the telescope is reached. It is calculated as:

This corresponds more or less to a factor X of 1.5 (exact: 1.43) in the first formula.

Note: For small-scale deep-sky objects Stoyan (Deep Sky Guide) proposes to go far beyond the beneficial visual power up to the maximum visual power.

Maximum Magnification

For small-scale deep-sky objects Stoyan (Deep Sky Guide) proposes to go far beyond the beneficial visual power up to the maximum magnification, which is twice as high as the beneficial visual power (and corresponds to a factor X of 3). Depending on the telescope type and the seeing (air turbulence), this is, however, not always possible. Smaller telescopes reach their maximum visual power easier because it is lower than that of large telescopes and thus, the seeing has less influence.

Minimum Useful Magnification

The minimum (useful) magnification is characterized as: the exit pupil of the telescope and the eye pupil are of the same size, so no light is lost. Depending on the source, values between 5 mm and 8 mm are used for the eye pupil. Typically, however, calculations use a value of 7 mm or 6.5 mm.

The minimum useful magnification (normal magnification) is determined by the size of the exit pupil:

If magnification is too low, parts of the light that leaves the eyepiece cannot be utilized by the human eye (the exit pupil is too large).

Mount (Telescope Mount)

A telescope mount is a mechanical structure which supports a telescope. Telescope mounts are designed to support the mass of the telescope and allow for accurate pointing of the instrument. Many sorts of mounts have been developed over the years, with the majority of effort being put into systems that can track the motion of the stars as the Earth rotates. (From Wikipedia)

Popular mounts are:

Newtonian Telescope/Reflector

The Newtonian telescope (or reflector) is a type of reflecting telescope invented by the British scientist Sir Isaac Newton (1642–1727), using a concave primary mirror and a flat diagonal secondary mirror. Newton’s first reflecting telescope was completed in 1668 and is the earliest known functional reflecting telescope. The Newtonian telescope's simple design makes it very popular with amateur telescope makers.
(From Wikipedia)

Resolution, Resolving Power

Resolution (or resolving power) is defined as the ability to separate two closely spaced objects (e.g., binary stars in astronomy). There are two empirically found criteria for this ability:

In the practice, rules of thumb are used for both criteria. That is why I leave out the complex mathematics here. The two rules of thumb are:

The resolution depends solely on the aperture of the telescope. Obviously, the Dawes criterion is considered "more practical" (see the article by Stefan Gotthold), and the manufacturers also provide this value (probably also because it looks better).

Example Table: Resolution Values Given by the Manufacturers and the "Rule of Thumb" Formulae

Telescope Focal Length * Aperture Rayleigh Dawes Manufacturer
Refractor 400...700 60 2.3" 1.93"  
S-W Heritage 76 300 76 1.82" 1.53" 1.51"
Refractor 500...900 80 1.725" 1.45"  
Meade ETX 90EC 1250 90 1.53" 1.29" 1.3"
S-W Heritage 100P 400 100 1.38" 1.16" 1.15"
S-W Skymax-102 1300 102 1.35" 1.14" 1.15"
S-W Skymax-127 1500 127 1.08" 0.91" 0.91"
S-W Explorer 150PDS 750 150 0.92" 0.77" 0.77"
GSO GSD 680 1200 200 0.69" 0.58" 0.58"
Meade Lightbridge 10" 1270 254 0.54" 0.46" 0.45"

*) Not needed here

Note: Normally, resolution is limited to about 1" due to air turbulence in the atmosphere. Only in rare exceptional cases, it is better. Thus, telescopes having an aperture of more than 120 mm* will not produce any real advantage with respect to resolution (Astroshop, Oden).

*) 120 mm seems to refer to Dawes criterion.

Resolution for the Moon

The above resolution formulae apply to fine structures such as double stars. In his book Moonhopper, Lambert Spix provides the following empirically determined formulae for the moon, which correspond to much higher resolutions, i.e. enable capturing much smaller structures:

According to Spix, these "theoretic" values have to be doubled in most nights due to atmospheric turbulence. Structures below 0.16" (300 m) are practically invisible even with large telescopes (larger than 10").

Example Table: Resolution Values and Doubled Resolution Values Calculated According to the "Empirical Formulae"

     
Theoretical
Doubled
Telescope Focal Length * Aperture Crater Groove Crater Groove
Refractor 400...700 60 0.65" 0.38" 1.30" 0.76"
S-W Heritage 76 300 76 0.51" 0.30" 1.03" 0.61"
Refractor 500...900 80 0.49" 0.29" 0.98" 0.58"
Meade ETX 90EC 1250 90 0.43" 0.26" 0.87" 0.51"
S-W Heritage 100P 400 100 0.39" 0.23" 0.78" 0.46"
S-W Skymax-102 1300 102 0.38" 0.23" 0.76" 0.45"
S-W Skymax-127 1500 127 0.31" 0.18" 0.61" 0.36"
S-W Explorer 150PDS 750 150 0.26" 0.15" 0.52" 0.31"
GSO GSD 680 1200 200 0.20" 0.12" 0.39" 0.23"
Meade Lightbridge 10" 1270 254 0.15" 0.09" 0.31" 0.18"

*) Not needed here; 0.52" roughly corresponds to 1 km on the moon.

Resolution and Photography

To exploit a particular resolution, you need a sensor with at least two pixels within the distance that corresponds to the resolution. For this, imagine the focal length as the radius of a circle with 360°, 1° is then 1/360 of it, 1' is 1/60 of this, and finally 1" is again 1/60 of this. Multiply the actual resolution value in arc seconds with the 1" value to determine the distance that corresponds to the resolution value and then compare it to the pixel size of the sensor used or of other sensors.

Examples:

These estimates were done according to the article Was ist eigentlich ... die Auflösung? by Peter Oden. The examples use the Rayleigh resolutions of the telescopes.

Human Eye

The human eye has resolution of about 1' (practically, theoretically it is 20"). For practical astronomical applications, often a value of 2' or even 3' is given.

(After: Was ist eigentlich ... die Auflösung? (Peter Oden, Abenteuer Astronomie) und Mathematik in der Astronomie (Teil 4): Das Auflösungsvermögen von Teleskopen (Stefan Gotthold, clearskyblog))

Right Ascension

Right ascension (abbreviated RA; symbol α) is the angular distance measured eastward along the celestial equator from the vernal equinox to the hour circle of the point in question. When combined with declination, these astronomical coordinates specify the direction of a point on the celestial sphere in the equatorial coordinate system.

An old term, right ascension (Latin, ascensio recta) refers to the ascension, or the point on the celestial equator which rises with any celestial object, as seen from the Earth's equator, where the celestial equator intersects the horizon at a right angle. It is contrasted with oblique ascension, the point on the celestial equator which rises with a celestial object as seen from almost anywhere else on Earth, where the celestial equator intersects the horizon at an oblique angle.
(From: Wikipedia)

Figure: Equatorial coordinate system (Source: Wikipedia, original uploader: Sverdrup (changed the original by Ulrich.fuchs), under CC license)

See also Equatorial Coordinate System

Seeing

Seeing means the air turbulence, mainly in the air layer near the ground, but also in the telescope dome and its direct surroundings, that we perceive with the naked eye as the flickering of the stars. The stronger the stars flicker, the worse is the seeing.

When observed visually in the telescope, seeing is expressed in a fraction of a second by the star dancing back and forth quickly, and in some weather conditions also by a blurred image. In astrophotography it enlarges the almost point-shaped star disk depending on the duration of the exposure time.

Seeing negatively affects the resolution and sharpness of visual observations and of astro photos by smearing fine details of the sun, moon, and planets when the seeing is bad. Consequently, the maximum useful magnification is also determined by the seeing: The worse the seeing is, the lower the magnifications that can be used. On nights with bad seeing it may therefore be impossible to visually and photographically obtain sharp images. However, this applies only to finely textured objects such as the sun, moon, planets, and double stars.

Seeing is also the measure of image blur caused by air turbulence. It is normally given in arc seconds and is often measured over the half-width FWHM (Full width at half maximum) of the image of a point source (e.g. a remote star).
(From www.hobby-astronomie.com, adapted and translated; Wikipedia: Seeing, adapted and translated)

Visual Power

See magnification

 

References

 

An den Anfang   Homepage  
gerd (at) waloszek (dot) de

About me
made by walodesign on a mac!
22.12.2024