Sony RX100 M1: Merklinger Apertures

On this page, I present a table of "Merklinger apertures" for the Sony RX100 M1 that was calculated using Excel. The calculations are based on formulae from Harold M. Merklinger's paper The INs and OUTs of Focus - An Alternative Way to Estimate Depth-of-Field and Sharpness in the Photographic Image (Internet edition).

Note: For more information, see my general page Merklinger's Approach to Estimating Depth of Field.

Introduction

In his article Hyperfocal distances and Merklinger's method in landscape photography, Kevin Boone discusses hyperfocal distance versus Harold M. Merklinger's approach to estimating depth-of-field in landscape photography. Boone's briefly describes Merklinger's method for scenes with distant objects as follows:

Focus on the most distant object in the scene, and set an aperture whose diameter is equivalent to the disk of confusion. The disk of confusion is the smallest distance between objects in the scene that need to be resolved.

For those, who just want to use this approach, Boone's article provides already the most important things that you need to know. There, you can find tables that help you employ the method (including added minimum distances from conventional DOF tables), as well as a discussion about the traditional approach to depth of field and hyperfocal distance calculations versus Merklinger's approach.

This page is directed at those, who want to use this approach with the Sony RX100 M1. I list a table of so-called "Merklinger apertures" that I calculated for this camera at various focal lengths and point to the table of hyperfocal distances for determining the corresponding "allowable" minimum distances. Finally, I list a simple procedure how the table can be used.

Table

The following table lists disks of confusion (distance set to infinity) for the Sony RX100 M1 at different focal lengths. This allows you to find the suitable "Merklinger apertures" in steps of one-third f-numbers.

Focal Length		f-Number
Actual	Equiv.	Nominal >	1.8	2	2.2	2.5	2.8	3.2	3.5	4	4.5	5.0	5.6	6.3	7.1	8	9	10	11
		Exact >	1.78	2	2.24	2.52	2.83	3.17	3.56	4	4.49	5.04	5.66	6.35	7.13	8	8.98	10.08	11.31
10.4	28	Diameter of Disk of Confusion (mm) >	5.84	5.20	4.63	4.13	3.68	3.28	2.92	2.60	2.32	2.06	1.84	1.64	1.46	1.30	1.16	1.03	0.92
13.0	35		7.30	6.50	5.79	5.16	4.60	4.09	3.65	3.25	2.90	2.58	2.30	2.05	1.82	1.63	1.45	1.29	1.15
18.5	50		10.38	9.25	8.24	7.34	6.54	5.83	5.19	4.63	4.12	3.67	3.27	2.91	2.60	2.31	2.06	1.84	1.64
25.9	70		14.54	12.95	11.54	10.28	9.16	8.16	7.27	6.48	5.77	5.14	4.58	4.08	3.63	3.24	2.88	2.57	2.29
37.1	100		20.82	18.55	16.53	14.72	13.12	11.69	10.41	9.28	8.26	7.36	6.56	5.84	5.21	4.64	4.13	3.68	3.28

Note: I determined the following maximum aperture values for the Sony RX100 M1 (equivalent focal lengths): 28 mm: f/1.8, 35 mm: f/2.8, 50 mm: f/3.2, 70 mm; f/4.0, 100 mm: f/4.9 (f/4.9 starts between 70 mm and 100 mm).

The diameters were calculated according to the formula d = f / N (d = diameter of disk of confusion = diameter of working aperture; f = focal length; N = f-number), which is valid for distance set to infinity. The exact f-numbers were used in the calculations.

Further down, I present a simple procedure how the table can be used.

Diagram

The following diagram was created from the table above using Excel:

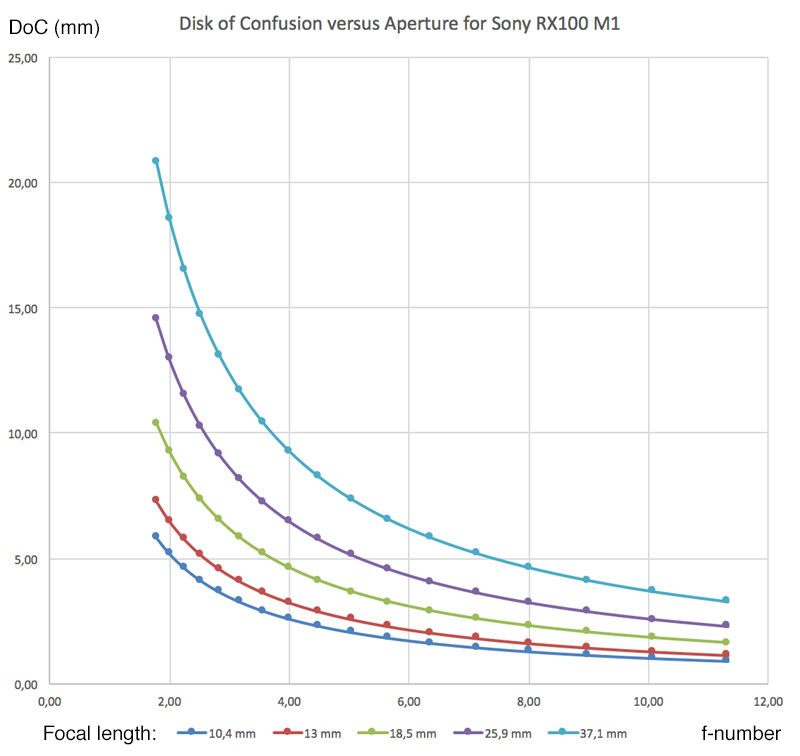
Diagram: Merklinger apertures for the Sony RX100 M1 (distance set to infinity)

Determining the "allowable" Minimum Distance

You can determine the "allowable" minimum distance on the basis of traditional calculation tables (or the DOF markers on the lens - but the Sony RX100 M1 has none...). As Merklinger shows for the traditional DOF calculations (p. 15) and I found out myself independently using Merklinger's approach, the hyperfocal distance (HFD) is the minimum distance (based on the CoC criterion) for a given "Merklinger aperture", when the lens is focused at infinity.

Thus, for determining the minimum distance for the RX100 M1, just look at my table for hyperfocal distances for this camera. Also note that at half the hyperfocal distance, the disk of confusion is half the size of the diameter of the working aperture, meaning the CoC is about double the "allowed" size. This leads to a decrease in resolving power in the object field and a decrease in conventional sharpness in the image (CoC and DoC are proportional to each other*).

*) The formula is: Sx = c * X / f (focus D on infinity, X = object distance; c = diameter of circle of confusion; Sx = diameter of disk of confusion; f = focal length of lens)

In short: When focusing at infinity and setting the "Merklinger aperture", the CoC has its "nominal" (= allowable) size at HFD and double its "nominal" size at HFD/2.

Procedure

With distance set to infinity, you can employ a "special case" of the "Merklinger approach" suitable for landscape photography (no important objects in the close foreground) by following these steps:

Choose a diameter for the disk of confusion based on the size of the features in the images to be resolved; this is also the diameter for the working aperture.
Select from the d-value table an appropriate f-number for the focal length of the lens that you will use*. Round in the direction of a larger f-number to be "on the safe side".
Take care that the aperture-number is not above f/8 to prevent softness from diffraction (details).
Go to the table of hyperfocal distances, look for the focal length and f-number to be used and determine the hyperfocal distance. This can be used as "allowable" minimum distance based on the traditional CoC criterion.

*) For my tables, I used fixed f-numbers, as given by the cameras, and the most important focal lengths of my cameras to calculate tables of d-values. When you use these tables, you first have to decide on a value of d based on the scene to be photographed and a focal length and then search the table for a suitable d-value and extract the corresponding f-number for that focal length. Often, you will not find the exact d-value in the table and have to decide for one that comes close. Choose the f-number conservatively in this case, that is, select the next larger f-number to be "on the safe side".

How to Use the Tables for Finite Distances

Can you use the f-numbers that I calculated for the infinity condition also for finite distances? The answer is "yes" if you are willing to do some simple calculations - in your head or using a calculator: Just calculate or estimate (X - D) / D and multiply the f-number for infinity with it - voila! It's even simpler for fractions of D. Here are the formulae:

Near Limit: X < D
Sx = (D - X) / D * d => Factor: (D - X) / D or (1 - X/D)
if X = D/n you get for the factor: (1 - 1/n) => the closer X goes to 0, the larger n gets => Sx approaches d
Far Limit (if to be specified separately): Y > D
Sy = (Y - D) / D * d => Factor: (Y - D) / D or (Y/D - 1)
if Y = n*D you get for the factor: (n - 1) => the larger Y gets, the larger n gets => Sy goes beyond all limits

Examples:

For X = D/2 you get a factor of 2, meaning that the table values can be divided by 2
For Y = 2*D, you get a factor of 1, meaning that the table values can be used directly

Conclusions

Using the table of "Merklinger apertures" on this page and the table of hyperfocal distances for the Sony RX100 M1, you can employ a "special case" of Merklinger's approach, where distance is set to infinity, which is well suited to landscape photography. But with a little bit of math, you can also use the table for finite focus distances.

References

Kevin Boone: Hyperfocal distances and Merklinger's method in landscape photography (www.kevinboone.net/hyperfocal.html)
Harold M. Merklinger: The INs and OUTs of Focus - An Alternative Way to Estimate Depth-of-Field and Sharpness in the Photographic Image (Internet edition; www.trenholm.org/hmmerk/TIAOOFe.pdf)
Harold M. Merklinger: Depth of Field Revisited (www.trenholm.org/hmmerk/DOFR.html)