Leica X Vario: Hyperfocal Distance

Introduction | Table | Diagram | Conclusions | References

Archive

On this page, I present tables of the hyperfocal distance for the Leica X Vario using Excel. The table calculations are based on formulae that I found on the DOFMaster Website and described on page Calculating Hyperfocal Distance and Depth of Field.

Note that the tables can also be used for a simplified version of the Merklinger method for determining depth of field, where distance is set to infinity. Then, the hyperfocal distance is the "near limit" according to the conventional approach based on the circle of confusion (the Merklinger approach does not provide such a near limit).

See the notes on page A Small Glossary of Photography Terms regarding the validity of depth of field and hyperfocal distance calculations as well as of the circle of confusion, on which these calculations are based.

Note: I hit on a discusion in the l-camera-forum that DOF is different for digital cameras than for analog (film) cameras. According to an article, entitled Profondeur de champ et capteurs numériques (English version: Depth of field and digital sensors) that was cited there, the CoC is to be calculated as the photosite size multiplied by a factor of 1.5 However, before I create new tables, I will first wait how this issue is further discussed in the above-mentioned thread...

Note: For details, see my general page Calculating Hyperfocal Distance and Depth of Field.

Introduction

The hyperfocal distance is useful for shooting with manual focus and aperture. When you set a lens to the hyperfocal distance, everything will be sharp from half the hyperfocal distance to infinity. Sharpness is defined by the circle of confusion (CoC). It is typically set to 0.025 mm for APS-C sensors, but Leica sets it at 0.02 mm for the Leica X Vario (it seems to set it to 0.019 for a focal length of 18 mm).

The hyperfocal distance depends on three factors:

Focal length (the exact length, not the equivalent length),
Aperture (f-number),
Circle of confusion (CoC).

I present the formulae for calculating the hyperfocal distance on page Calculating Hyperfocal Distance and Depth of Field.

You can calculate the hyperfocal distance for a given focal length and aperture using DOFMaster. Set the circle of confusion to 0.02 mm or 0.019 mm for a focal length of 18 mm.

Examples:

18 mm, f/3.6, 0.02 mm: 4.56 m (2.28 m to infinity); 18 mm, f/3.6, 0.025 mm: 3.65 (1.825 m to infinity)
44.7 mm, f/6.4, 0.02 mm: 15.8 m (7.9 m to infinity); 44.7 mm, f/6.4, 0.02 mm: 12.6 m (6.3 m to infinity)

Please note that the values f/3.5 and 44.6 mm are not available in DOFMaster.

For the Leica X Vario, you can also determine the hyperfocal distance "after the fact" by inspecting an image's Exif data using ExifTool or other tools that use the ExifTool engine. They are listed in the "Composite" section, which are useful parameters that ExifTool calculates from other data. Here, a circle of confusion of 0.02 mm is listed (0.019 mm for a focal length of 18 mm).

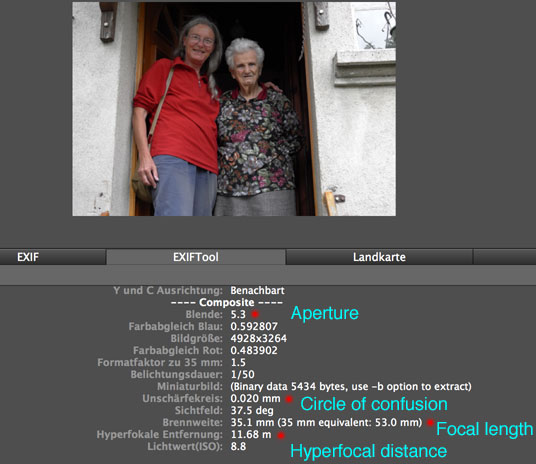
Figure 1: Inspecting Exif data in GraphicConverter for the hyperfocal distance and the circle of confusion

In the following, I present my own calculations of the hyperfocal distance and offer them in tabular and graphical format.

Table

The following table shows the hyperfocal distance for the Leica X Vario based on a circle of confusion (coc) of 0.02 mm and one-third f-numbers (because you can set these on the Leica X Vario's aperture dial). For a focal length of 18 mm, however, Leica lists a coc of 0.019 mm. Therefore, the table includes a column with a coc of 0.019 mm for the focal length of 18 mm. It's up to you, which CoC you will use for 18 mm...

		Focal Length
		1.56	1.56	1.52	1.52	1.52	Crop Factor
f-Number		28	28	35	50	70	Equivalent
Nominal	Exact	18	18	23	33	46	Actual
3.5	3.56	4.80	4.56	7.45	15.31	29.74
4	4.00	4.28	4.07	6.64	13.65	26.50
4.5	4.49	3.82	3.63	5.91	12.16	23.61
5.1	5.04	3.40	3.23	5.27	10.84	21.04
5.6	5.66	3.03	2.88	4.70	9.66	18.75
6.4	6.35	2.70	2.57	4.19	8.61	16.71
7.1	7.13	2.41	2.29	3.73	7.67	14.89
8	8.00	2.15	2.04	3.33	6.84	13.27
9	8.98	1.92	1.82	2.97	6.10	11.83
10	10.08	1.71	1.63	2.65	5.44	10.54
11	11.31	1.53	1.45	2.36	4.85	9.40
12.7	12.70	1.36	1.29	2.11	4.32	8.38
14	14.25	1.21	1.15	1.88	3.85	7.47
16	16.00	1.08	1.03	1.68	3.44	6.66
Circle of confusion		0.019	0.02	0.02	0.02	0.02

Note that only the light gray values can be used on the X Vario. The darker gray values are out of the scope of the lens because of its variable aperture. Moreover note that there are no markers between 4 m and infinity. Thus, setting a distance larger that 4 m may become a matter of luck (or experimentation using my secret Exif fields)...
(I determined the following maximum aperture values (equivalent focal lengths) for the Leica X Vario: 28 mm: f/3.5, 35 mm: f/4.5, 50 mm: f/5.1, 70 mm: f/6.4 (f/6.4 starts between 50 mm and 70 mm)).

Also remember that sharpness extends from half the hyperfocal distance to infinity.

Diagram

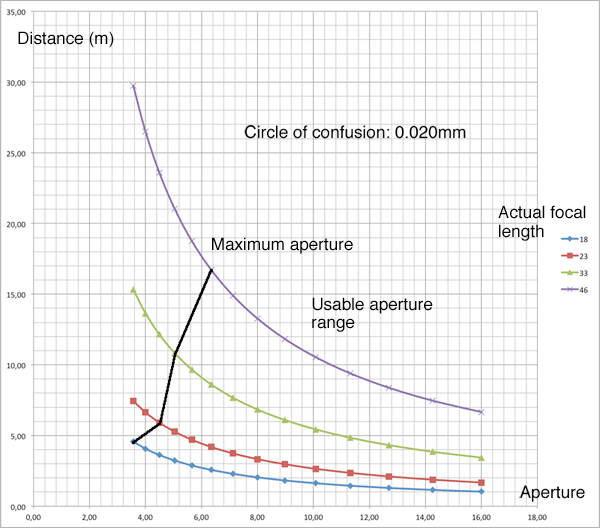
Tables show exact numbers, but are hard to read. I therefore also created a graphic from the table (coc = 0.02 mm) and annotated it using Adobe PSE:

Figure 2: Diagram of hyperfocal distances depending on focal length and f-number for the Leica X Vario (coc = 0.02 mm; click the graphic for a larger version)

The dark black line indicates the maximum aperture (or f-number). The usable aperture range is to the right of this line. This line suggests that for a focal length of 35 mm (equivalent), the maximum f-number should be 4 - but the camera indicates 4.5.

Conclusions

The distance scale on the Leica X Vario has a very limited set of values beyond 1m: 1.5, 2, 4, and infinity. Therefore, it is difficult to set the distance ring to an "estimated" value of, for example, 10 m. I have no idea, what distance setting the distance ring to the middle between 4 m and infinity really comes up. I might check this using the (deciphered) Exif data, but from my experience I assume that I will get a huge variation between the values...

All in all, I find the usefulness of these calculations rather limited, particularly considering the design of the lens' distance scale. Nevertheless, here are some of my "key findings":

70 mm (equiv. = 46 mm): Using the hyperfocal distance does not make sense because it is difficult to reliably set a distance between the 4 m and infinity marks
50 mm (equiv. = 33 mm): At f/14 you reach the magical "4 m" mark. This does not make much sense, either...
35 mm (equiv. = 23 mm): At about f/6.4 you reach the magical "4 m" mark. Thus, setting distance a little bit beyond 4 m and aperture to f/6.4 can be useful in certain cases.
28 mm (equiv. = 18 mm): At f/4 you come close to the magical "4 m" mark. Thus, you can set aperture to f/4 and distance to 4 m or a little bit beyond, or you use f/3.5 and move the distance ring a little bit more beyond 4 m to set the hyperfocal distance (meaning that you will get everything sharp from 2 or 2.5 m to infinity). Both settings may be useful options for street photographers.

References

DOFMaster Website
Schärfentiefe und Bokeh by H. H. Nasse, Zeiss, 2010; in German
Profondeur de champ et capteurs numériques (English version: Depth of field and digital sensors)
Profondeur de champ (DOF calculator, French), version 1.6