General: Calculating Object Diameter and Angle of View, Minimum Object Size, and Magnification

Calculating Object Diameter and Angle of View from Distance | Calculating Minimum Object Size and Magnification for Full Format | Calculating Minimum Object Size and Magnification for APS-C Format

On this page, I demonstrate how you can calculate object diameter, minimum object size, and magnification of lenses for full and APS-C format cameras/sensors. This page supplements pages where I determine this data for my M-mount lenses when used at the Ricoh GXR and the Leica M (Typ 240).

Calculating Object Diameter and Angle of View from Distance

Sharpness and resolving crtiteria for lenses and sensors are often given in angular measurements. For example, the human eye is said to have a resolving power of one minute of an arc. This criterion was relaxed to 2 minutes of an arc for determining the circle of confusion (CoC), which is used in calculations of the hyperfocal distance (HFD) and the depth of field (DoF). But knowing an angle does not tell us the diameter of an object of that angular size at a certain distance (or simpler, how wide it is). In the following, I show how you can calculate the diameter at a certain distance.

The diagram below shows that the object diameter g is related to the angle of view a through the TAN function and scaled by the distance r:

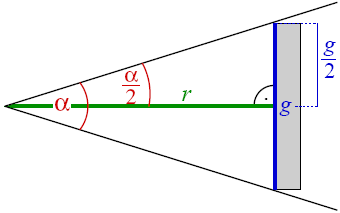
tan(a / 2) = (g / 2) / r => g = 2 * r * tan(a / 2)

Legend: r = (shortest) distance, g = object diameter, a = angle of view (alpha in diagram)

For the calculations, you need a calculator (or an Excel sheet). Here is an example table showing the diameters at different distances for the just mentioned 1 and 2 minutes of an arc, for 30' (the approximate angular size of the moon and the sun) and or 32' (the average angular size of the moon and the sun):

	Distance
Angle of View	m									km
Angle of View	0.25	0.5	1	2	5	10	20	50	100	1	10	100	1000	384,000	149,600,000
1'	0.073	0.145	0.291	0.582	1.454	2.9	5.8	0.0145	0.0291	0.2909	2.909	29.09	290.89	111.70	43,516.88
2'	*0.145*	*0.291*	*0.582*	*1.164*	*2.909*	*5.8*	*11.6*	*0.0291*	*0.0582*	*0.5818*	*5.818*	*58.18*	*581.78*	*223.40*	*87,033.75*
30'	2.182	4.363	8.727	17.453	43.634	87.3	174.5	0.4363	0.8727	8.7267	87.267	872.67	8726.70	3,351.05	1,305,514.57
32'	2.327	4.654	9.308	18.617	46.542	93.1	186.2	0.4654	0.9308	9.3085	93.085	930.85	9308.49	3,574.46	1,392,550.09
	mm							m						km
	Diameter

Legend:
Bold+italic: Viewing angle that corresponds to the CoC
Moon: distance = 384,000 km;diameter = 3,476 km; angular size ranges from 29.2' to 33.3' nearly 32' on average
Sun: distance = 149,600,000 km; diameter = 1,392,684 km; angular size ranges from 31.5' to 32.5', 32' on average
As you can see, the calculated values for diameters of the moon and sun come close to the real values.

A viewing angle of 2' corresponds to the "acceptable sharpness" criterion for the CoC, which is based on the resolving power of the human eye (1/8 mm at 25 cm viewing distance), but somewhat relaxed. 1' would correspond more closely to the actual resolving power of the human eye.

Note that the resolving power of astronomical telescopes is also given as an angle. I will use this information to calculate, which details (measured in km) my telescopes can resolve under optimal conditions on the moon and on the sun. Perhaps, a moon map can help me to find out what this actually means...

Viewing Angle from Distance

In some cases, it might also be useful to know the viewing angle a for an object with diameter g at a distance r. The viewing angle a is given by the following formula:

a = 2 * arctan(g / (2 * r))

Legend: r = (shortest) distance, g = object diameter, a = angle of view (alpha in diagram above)

For the calculations, you need a calculator (or an Excel sheet). Here is an example table showing the viewing angles in degrees (decimal...) for different distances and for different diameters in the millimeter range (which may correspond to aperture diameters):

	Distance
Diameter (mm)	m									km
Diameter (mm)	0.25	0.5	1	2	5	10	20	50	100	1	10	100	1000
0.125	0.029	0.014	0.007	0.004	0.001	0.0007	0.0004	0.0001	0.0001	0.000007	0.000001	0.00000007	0.00000001
0.145	0.033	0.017	0.008	0.004	0.002	0.0008	0.0004	0.0002	0.0001	0.000008	0.000001	0.00000008	0.00000001
0.25	0.057	0.029	0.014	0.007	0.003	0.0014	0.0007	0.0003	0.0001	0.000014	0.000001	0.00000014	0.00000001
0.5	0.115	0.057	0.029	0.014	0.006	0.0029	0.0014	0.0006	0.0003	0.000029	0.000003	0.00000029	0.00000003
1	0.229	0.115	0.057	0.029	0.011	0.0057	0.0029	0.0011	0.0006	0.000057	0.000006	0.00000057	0.00000006
1.5	0.344	0.172	0.086	0.043	0.017	0.0086	0.0043	0.0017	0.0009	0.000086	0.000009	0.00000086	0.00000009
2	0.458	0.229	0.115	0.057	0.023	0.0115	0.0057	0.0023	0.0011	0.000115	0.000011	0.00000115	0.00000011
3	0.688	0.344	0.172	0.086	0.034	0.0172	0.0086	0.0034	0.0017	0.000172	0.000017	0.00000172	0.00000017
4	0.917	0.458	0.229	0.115	0.046	0.0229	0.0115	0.0046	0.0023	0.000229	0.000023	0.00000229	0.00000023
5	1.146	0.573	0.286	0.143	0.057	0.0286	0.0143	0.0057	0.0029	0.000286	0.000029	0.00000286	0.00000029
10	2.292	1.146	0.573	0.286	0.115	0.0573	0.0286	0.0115	0.0057	0.000573	0.000057	0.00000573	0.00000057
20	4.581	2.292	1.146	0.573	0.229	0.1146	0.0573	0.0229	0.0115	0.001146	0.000115	0.00001146	0.00000115
25	5.725	2.864	1.432	0.716	0.286	0.1432	0.0716	0.0286	0.0143	0.001432	0.000143	0.00001432	0.00000143
50	11.421	5.725	2.864	1.432	0.573	0.2865	0.1432	0.0573	0.0286	0.002865	0.000286	0.00002865	0.00000286
100	22.620	11.421	5.725	2.864	1.146	0.5730	0.2865	0.1146	0.0573	0.005730	0.000573	0.00005730	0.00000573
	Viewing Angle (Degrees, decimal)

Legend:
Bold+italic: about 2' corresponding to the circle of confusion
Bold: about 1' corresponding to the limit of human resolviong power
red: about 1"

Notes: 1' = 0.016666, 2' = 0.033333 degrees in decimal notation

The table shows, among others, at about which distance the human eye can no longer resolve details of a certain diameter (this is reflected in the CoC, which is the basis for DoF scales on lenses and the hyperfocal distance). This information can also be used to estimate at what distance a disk of confusion, which is used in Merklinger's method, can no longer be resolved, albeit the theory, based on geometrical optics, would not take this into consideration.

Calculating Minimum Object Size and Magnification for Full Format

The following calculations are useful for lenses. For each lens, an angle of view (for an 36 x 24 mm image format) and a minimum (or shortest) distance is given in the technical data. This allows you to calculate the minimum object size and the magnification for a lens using some geometric relationships.

The diagram below shows that the object size g is related to the angle of view a through the TAN function and scaled by the distance r:

tan(a / 2) = (g / 2) / r => g = 2 * r * tan(a / 2)

Legend: r = (shortest) distance, g = diagonal object width, a = angle of view (alpha in diagram)

Since g is the diagonal object size, we need to calculate the width and height of the object rectangle. This is easy for the 3:2 image image format (w=3*a, h=2*a), which allow us to use the theorem of Pythagoras:

g*g = 3*3*a*a + 2*2*a*a = 15*a*a => g = sqr(15)*a => a = g/sqr(15)

Replacing a by g, we arrive at the following fomulae for object width w and object height h:

w = 3*a = 3*g/sqr(15)
h = 2*a = 2*g/sqr(15)

Inserting the formula for g, finally leads to formulae in which object width w and object height h depend only on distance r and angle a::

w = 3*2*r*tan(a/2)/sqr(15) = 6/sqr(15)*r*tan(a/2)
h =2*2*r*tan(a/2)/sqr(15) = 4/sqr(15)*r*tan(a/2)

Magnification is given by dividing the object width (36 mm for 35 mm film) through the image width w (analogously for the height h):

M = 36/w = 36*sqr(15)/(3*2*r*tan (a/2)) (mm) = 6*sqr(15)/(r*tan(a/2))

Take the inverse of M to arrive at the 1:X format:

X = r*tan(a/2)/(6*sqr(15))

Example (Zeiss Biogon 21mm f/4.5)

Angle of view a = 90 degrees, a/2 = 45 degrees, tan(45 degrees) = 1

Shortest Distance r = 500 (mm), sqr(15) = 3.873

w = 6/3.873*500 = 774.4 mm; h = 4/3.873*500 = 516 mm

M = 0.046 => M = 1: 21.5

(No responsibility is taken for the correctness of this information)

Calculating Minimum Object Size and Magnification for APS-C Format

In the case of an APS-C (or better, DX format) sensor, you can either:

Divide the angle of view by the crop factor or
Calculate the angle of view from the sensor format

and then use the formulae for full format described above.

The crop factor for APS-C (DX format) is typically given as 1.5. Since the sensor format is not exactly 24 x 16 mm (here, it use 23.6 x 15.7 mm, but I found several minor variants of this...), the second method would be a little more exact (1.525 for the width). The formula for the second approach uses the diagonal of the sensor and is as follows:

angle of view (diagonal) = 2 * ARCTAN (Sensor diagonal / (2 * focal length))

For the APS-C sensor size given above, the diagonal is about 28.35 mm.

For the APS-C sensor, I calculated the values from the same formulae, but used the adapted angle of view for the APS-C format.